A post on StackOverflow caught my eye, asking why calculating factorial(10_000) is roughly 4-5x faster in Python 3.2 than in Python 2.7. The answer points to an updated implementation of under-the-hood C code that uses a new algorithm.

In this post, we examine three approaches to computing factorials: traditional/recursive, Python’s divide-and-conquer, and prime factorization.

Factorials, the traditional way #

The factorial function is often a good example of coding with recursion. Since n! = n * (n-1)!, we can write a simple recursive algorithm in Python to calculate it:

def factorial_recursive(n):
  if n == 1:
    return 1
  return n * factorial_recursive(n - 1)

When we use recursion, we should be mindful of blowing up the call stack. Each function call needs its own frame for local variables and must know where to return, so memory usage will be higher.

Let’s rewrite factorial without using recursion. To do so, we make use of Python’s range, and multiply that in to our cumulative answer:

def factorial_basic(n):
  val = 1
  for i in range(n):
    val *= (i + 1) # take care of the off-by-one in range
  return val

All is good here, but since this post is about performance, let’s consider extremely large factorial calculations…

factorial(10) will return pretty quickly, but what about factorial(10_000)? And factorial(1_000_000)?

The number of multiplications we need will increase for larger inputs to the function. In fact, this relationship is linear: factorial(10) will require twice the number of multiplies as factorial(5). In big-O notation we’d write this as O(n). Linear algorithms aren’t bad, but can we do better?

Factorials, the Python way #

According to the source code, Python now uses a “divide and conquer” algorithm to get the factorial in the form: $$factorial(n) = 2^k * m\text{, m is odd}$$

Calculating 2^k is going to be much easier for binary computers since we just need some bit shifting. But why this special form? And how do we get a factorial into this form?

It will help to look at an example:

$$20! = \begin{smallmatrix} &1 &\cdot &2 &\cdot &3 &\cdot &4 &\cdot &5 &\cdot &6 &\cdot &7 &\cdot &8 &\cdot &9 &\cdot &10 & \cdot & \newline &11 &\cdot&12 &\cdot &13 &\cdot &14 &\cdot &15 &\cdot &16 &\cdot &17 &\cdot &18 &\cdot &19 &\cdot &20 &\end{smallmatrix}$$

Now let’s rearrange (since multiplication is commutative) to organize even and odd terms:

$$20! = \begin{smallmatrix} &1 &\cdot &3 &\cdot &5 &\cdot &7 &\cdot &9 &\cdot &11 &\cdot &13 &\cdot &15 &\cdot &17 &\cdot &19 & \cdot & \text{// odd terms}\newline &2 &\cdot&4 &\cdot &6 &\cdot &8 &\cdot &10 &\cdot &12 &\cdot &14 &\cdot &16 &\cdot &18 &\cdot &20 & & \text{// even terms} \end{smallmatrix}$$

Each even number contributes a factor of two, so we get:

$$20! = \begin{smallmatrix} &1 &\cdot &3 &\cdot &5 &\cdot &7 &\cdot &9 &\cdot &11 &\cdot &13 &\cdot &15 &\cdot &17 &\cdot &19 & \cdot & & \text{// odd terms}\newline & \color{DarkGreen} 2^{10} & [ & 1 & \cdot & 2 & \cdot & 3 & \cdot & 4 & \cdot & 5 & \cdot & 6 & \cdot & 7 & \cdot & 8 & \cdot & 9 & \cdot & 10 & ] \text{ // factor out 2} \end{smallmatrix}$$

And something exciting happens - after factoring out two from each even number, we notice a smaller factorial appears!

$$20! = \begin{smallmatrix} &1 &\cdot &3 &\cdot &5 &\cdot &7 &\cdot &9 &\cdot &11 &\cdot &13 &\cdot &15 &\cdot &17 &\cdot &19 & \cdot & \text{// odd terms}\newline & 2^{10} &\cdot & [ & \color{DarkRed} 10! & ] & & & & & & & & & & & & & & & & \text{ // a smaller factorial!} \end{smallmatrix}$$

On our first iteration of factoring out twos from the even numbers we now have ten. But notice that in the bottom row we’re now left with a 10!. There will be more factors of two in that bottom term, and we’ll need to repeat that step a few more times.

Leaving those steps as an exercise for the reader, we’ll arrive at:

$$20! = \begin{smallmatrix} &1 &\cdot &3 &\cdot &5 &\cdot &7 &\cdot &9 &\cdot &11 &\cdot &13 &\cdot &15 &\cdot &17 &\cdot &19 & \cdot & & & \text{// odd terms from 20!} \newline & 1 & \cdot & 3 & \cdot & 5 & \cdot & 7 & \cdot & 9 & \cdot & & & & & & & & & & & & &\text{// odd terms from 10!} \newline & 1 & \cdot & 3 & \cdot & 5 & \cdot & & & & & & & & & & & & & & & & & \text{// odd terms from 5!} \newline & 2^{18} & & & & & & & & & & & & & & & & & & & & & & \text{// twos from even terms} \end{smallmatrix}$$

After quite a few numbers, we now have the required form:

$$factorial(20!) = 2^k * m_{odd} = 2^{18} * 9,280,784,638,125$$

A check on WolframAlpha confirms this math is correct, which is good news.

Admittedly that did seem longwinded, especially for a relatively small factorial such as 20!. Was it worth it?

Well, the above example is a manual illustration of what can be automated quite fast by a computer. For smaller factorials, it will be quicker to avoid the overhead of calculating the “even parts” and “odd parts”. But for larger factorials, there will be a payoff when we rely on bitshifting the two term instead of multiplying many terms.

There’s still more to squeeze out of this idea though. If our approach was to factor out all the twos we could from the factorial, why not do it for all primes? After all, the “odd part” in the above form felt like we weren’t giving it love - we simply swept up those terms as if they were insignificant add-ons.

We started by observing that every 2nd term contributes a factor of two. That same logic applies to every 3rd term contributing a factor of three, and every 5th term contributing a factor of five, etc. (We can skip composite numbers like “every 4th term” because they will be taken into account by their prime constituents.) Let’s move on to the prime factorization method.

Factorials using prime factorization #

The fundamental theorem of arithmetic states that any integer greater than one can be written as the product of prime numbers.

Let’s reconsider a smaller factorial, 6!, in terms of its prime factor form:

$$6! = 1 \cdot 2 \cdot 3 \cdot 4 \cdot 5 \cdot 6 = 2^a 3^b 5^c$$

The problem now becomes, how can we determine the powers a, b, and c? And can we do it without going through that long ruck we did in the previous section? As it turns out: yes, it’s actually quite easy!

How many factors of two do we need? Well we know that every even term in the product will contribute a factor.

$$6! = 1 * \overbrace{2}^{\text{factor of 2}} * 3 * \overbrace{4}^{\text{factor of 2 (twice)}} * 5 * \overbrace{6}^{\text{factor of 2}}$$

Therefore, we must have at least 6 / 2 factors of two, which in this case would be 3.

However, we forgot to count the fact that multiplying by 4 contributes a factor of two twice. So we need to add another factor for every power of two squared, 6 / 4.

We would need to then consider the numbers that are triply contributing a factor of two (that is, divisible by 8 = 2 * 2 * 2), but at this point there are no such numbers because we’ve exceeded the size of the input, which is 6.

We also need to take care that when calculating the number of factors, we round down when dividing. For example, when considering how many factors of two there are in 7!, otherwise we’d end up with a fractional exponent: (7 / 2) = 3.5.

So for any given prime, we can now calculate what the exponent should be in the factorial’s prime factor form via a formula known as Legendre’s Formula.

$$\upsilon_p(n) = \sum_{i=1}^{\left\lfloor{log_p(n)}\right\rfloor}{\left\lfloor{\frac{n}{p^i}}\right\rfloor}$$

Equipped with the ability to compute the exponents in the factorial’s prime factor form, let’s look at a practical example.

Example: write 6! = 720 in prime factor form

1. Establish the general form by writing n! as the product of primes. The primes will go up to n. $$6! = 2^a 3^b 5^c$$

2. Calculate the exponents via Legendre’s Formula, as written above, for each of the primes 2, 3, 5: $$a = \upsilon_2(6) = \left\lfloor \frac{6}{2^1} \right\rfloor + \left\lfloor \frac{6}{2^2} \right\rfloor = 4$$ $$b = \upsilon_3(6) = \left\lfloor \frac{6}{3^1} \right\rfloor = 2$$ $$c = \upsilon_5(6) = \left\lfloor \frac{6}{5^1} \right\rfloor = 1$$

   Therefore, 6! can be written as: $$6! = 2^4 \cdot 3^2 \cdot 5^1$$

Performance #

Let’s compare the performance of a basic factorial implementation (from the first section) versus factorials using prime factorization. (Python’s “divide and conquer” algorithm is left as an exercise for the reader, which will help familiarize you with their codebase.)

Basic factorial #

def factorial_basic(n):
  val = 1
  for i in range(n):
    val *= (i + 1)
  return val

Factorial using prime factorization #

The strategy here is:

1. Express the factorial in prime factorization form
   • To obtain primes up to N, we draw on 3rd party code
2. Use exponentiation by squaring to quickly calculate large exponents
   • This algorithm is not explained in this post, but there is a Computerphile video that explains it well

This code requires numpy.

import numpy

def primes_up_to(n):
  # `primefaster` by Takahashi Akari <akaritakahashioss@gmail.com>
  # https://github.com/takahashi-akari/prime-faster/blob/main/primefaster/primefaster.py
  if n < 2:
    return []
  if n == 2:
    return [2]
  if n == 3:
    return [2, 3]
  n += 1
  sieve = numpy.ones(n // 3 + (n % 6 == 2), dtype=bool)
  for i in range(1, int(numpy.sqrt(n)) // 3 + 1):
    if sieve[i]:
      k = 3 * i + 1 | 1
      sieve[k * k // 3 :: 2 * k] = False
      sieve[k * (k - 2 * (i & 1) + 4) // 3 :: 2 * k] = False
  np = numpy.r_[2, 3, ((3 * numpy.nonzero(sieve)[0][1:] + 1)|1)]
  return np.tolist()

def legendre(num, prime):
  denominator = prime
  total = 0
  
  while denominator <= num:
    total += num // denominator
    denominator *= prime
  
  return total

def fast_exponentiate(num, exp):
  # Square & Multiply Algorithm - Computerphile
  # https://www.youtube.com/watch?v=cbGB__V8MNk
  val = num
  for bit in bin(exp)[3:]:  # ignore '0b' prefix and first bit
    # square-multiply algorithm: 1=SM, 0=S
    val = val ** 2
    val *= num if bit == '1' else 1
  return val

def factorial_using_primes(n):
  val = 1
  for prime in primes_up_to(n):
    val *= fast_exponentiate(prime, legendre(n, prime))
  return val

To obtain the time it takes to run each function, we use Python’s timeit module. Performance will vary based on your specific hardware.

import timeit
for FACTORIAL_NUM in [1_000, 10_000, 20_000, 30_000, 40_000, 50_000, 100_000, 150_000, 200_000, 300_000, 400_000, 500_000]:
  print('factorial_basic', timeit.timeit('factorial_basic(FACTORIAL_NUM)', number=10, globals=globals()))
  print('factorial_using_primes', timeit.timeit('factorial_using_primes(FACTORIAL_NUM)', number=10, globals=globals()))

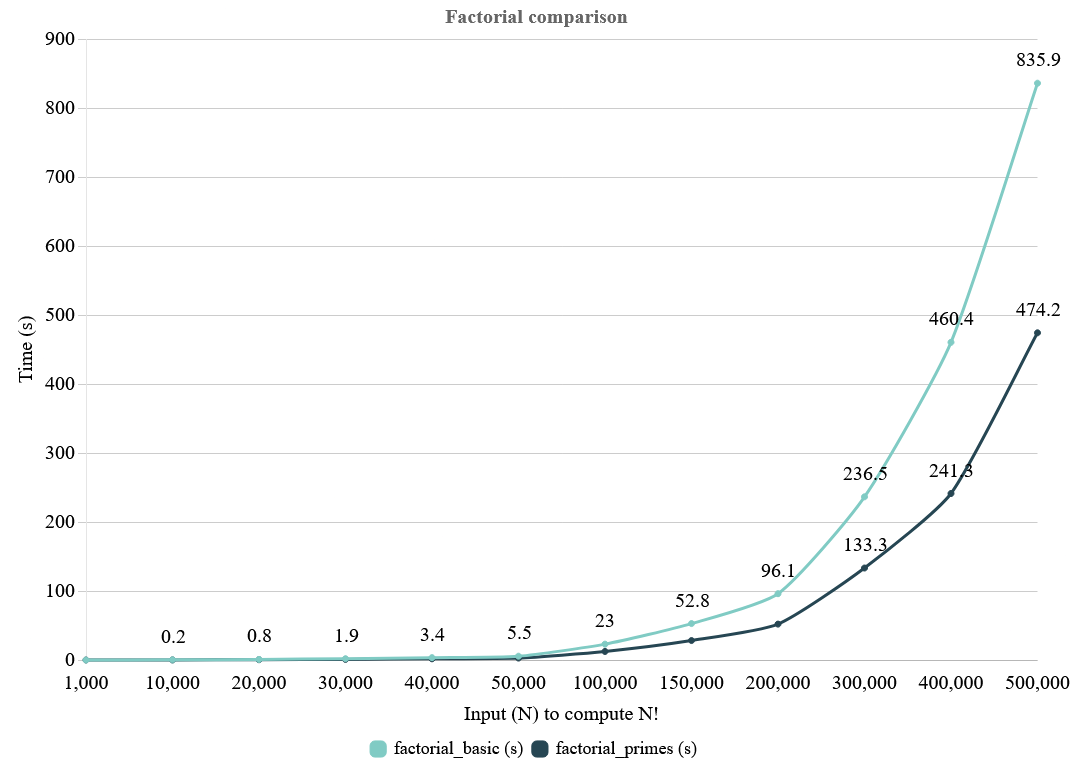
The prime factorization method outperforms the basic method by a factor of two (2x).

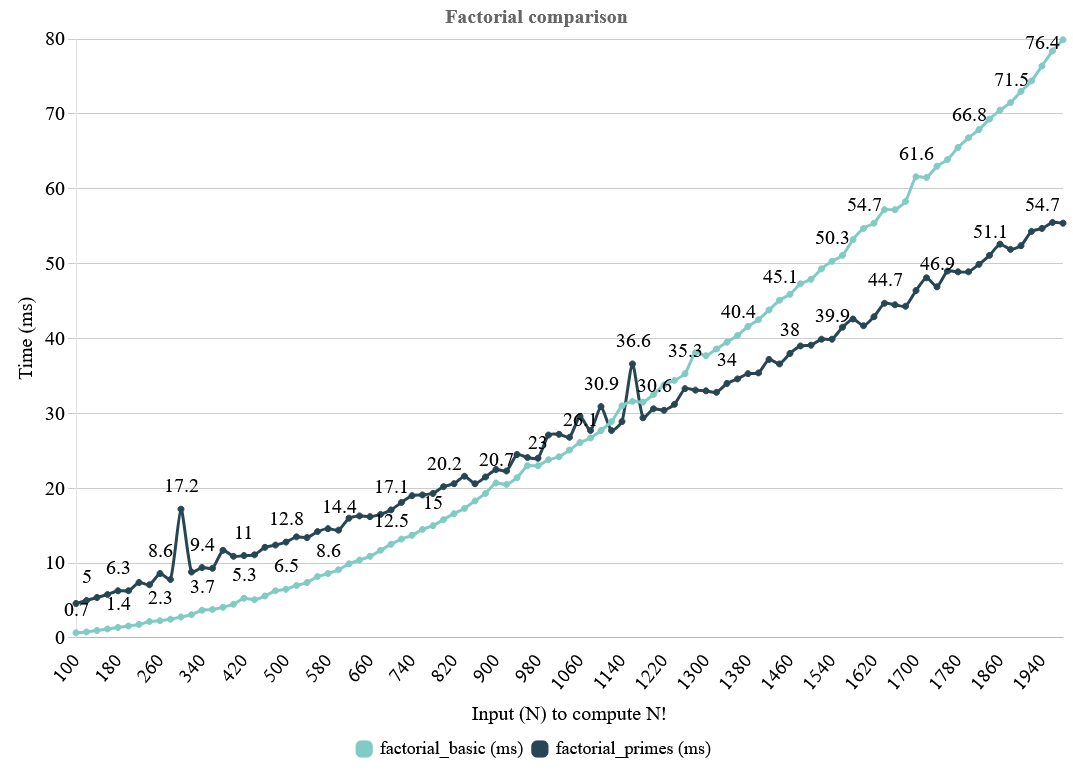
It’s hard to see in this chart where the prime factorization method overtakes the basic method. Using smaller inputs to see where the threshold is, we see it is around 1100! (at least on my machine) that both methods break even, and afterward the prime factorization method handily wins.

Conclusion #

We analyzed the performance of three different methods of computing a factorial. To improve performance for larger factorials, we turned to mathematics and techniques like prime factorization and exponentiation by squaring.

Is there ever a need to calculate factorials this large? Probably not, but the techniques applied in this post may help you in other programming endeavors, and hopefully you had fun along the way!

Thoughts or comments on this post? Send me an email at greg@greglang.me!